


Next: OpenMath and MathML
Up: The OpenMath Project Final
Previous: Technical Summary
Contents
Subsections
The OpenMath Standard
A lot of the mathematics online has until recently been presented
using the de-facto standard LaTeX (or TeX) despite the well known
limitations it has in handling interactivity. Documents generated by
transforming TeX sources to various flavors of HTML support only
cross-linking mechanisms and produce, in most cases, images for
formulae. More adventurous authors have included interactivity in the
form of plug-ins or JAVA applets in their pages. In the past three
years things have changed and new web technologies have established
themselves. In particular, the World Wide Web Consortium has published
the
recommendation for MathML,
the Mathematical Markup Language for
describing mathematical notation and capturing both its structure and
content [12]. Similarly, the OpenMath Society has endorsed
a newer version of
the OpenMath Standard
for representing the semantics
of mathematical objects and facilitating the exchange between computer
programs, the storage in knowledge bases, and the electronic
publication of mathematics [23]. In this document we
describe the OpenMath Standard.
By enabling mathematics to be served, received, and processed
electronically, both MathML and OpenMath aim at enhancing mathematical
communication on the on the World Wide Web just as hypertext has done
for text. The parallel evolution and definition of these predominant
markup languages for mathematics [17] resulted
in an ideal separation of complementary rôles: MathML presentation
can be used for presenting mathematical content written in OpenMath. The
major observation underlying this state of affairs is that
mathematics and its presentation should not be viewed as one and
the same thing. While the meaning of a mathematical object should
be uniquely defined and understood, its visualisation and rendering
depends on time and place, more precisely it depends on the context
and on the style preferences of the author or reader.
OpenMath is a language for representing and communicating
mathematics [11]. Originally, it
was conceived as a language for all computer algebra
packages [26,23]. Presently it is
equipped for conveying mathematical concepts arising from all areas of
mathematics, for instance logic. Now OpenMath can be used to express
formal mathematical objects, so that formal theorems and proofs,
understandable to proof checkers, can be communicated, as well as the
usual mathematical expressions handled by computer algebra packages.
In order to represent mathematical content it is crucial that a
mechanism is established to allow for the introduction of new
concepts, since this activity is at the core of mathematics. The OpenMath
representation of mathematics relies for this task on a small set of
``expression tree'' constructors (application, binding, attribution
and error), on some basic objects (byte-arrays, strings, integers, IEEE
floats, variables), and on the usage of symbols defined in Content
Dictionaries. These are publicly available collections of mathematical
definitions, a sort of xml dictionary of mathematics. The
interested reader may find the latest versions of the
standard documents and the collection of public Content Dictionaries at
the OpenMath Society website.
There are several aspects of OpenMath. Those presented in this section
are: the architecture of how OpenMath views integration of computational
software, the OpenMath Standard, and the OpenMath Phrasebooks and tools.
The OpenMath Standard is concerned with the objects, their encodings, and
the Content Dictionaries. The reader is referred to
the OpenMath Standard
[23] for details.
OpenMath Architecture
The architecture of OpenMath is made up of three layers of representation
of a mathematical object: the private layer for the internal
representation, the abstract layer for the representation as an OpenMath
object, and the communication layer for translating the OpenMath object
to a stream of bytes. An application will generally manipulate
mathematical objects using its internal representation; it can convert
them to OpenMath objects and communicate them by using the byte stream
representation of OpenMath objects.
It is not within the scope of OpenMath to define how communication takes
place, or the behaviour of services running in an integrated mathematical
environment. OpenMath defines the structure and semantics of the objects
being exchanged, not the actions taken when an object is received. For
example, OpenMath can represent an integrand, and an algebra system might
try to evaluate it in closed form while a renderer might attempt to
print it on a screen. Therefore, OpenMath is one ingredient
among many others that are needed for achieving integration of
computational tools, see for example a description of
how OpenMath is being used in recent applications [10].
OpenMath objects are representations of mathematical entities that can be
communicated among various software applications in a meaningful way,
that is in such a way that their ``semantics'' are well-defined.
OpenMath provides basic objects
like integers, symbols, floating-point numbers, character strings,
byte-arrays, and variables, and compound objects: applications,
bindings, errors, and attributions. Content Dictionaries (CDs)
specify the meaning of symbols informally using natural language and,
optionally, they might formally assign type information in the
signature of the symbols. CDs are public and are used to represent the
actual common knowledge among OpenMath-compliant applications. A central
idea to the OpenMath philosophy is that CDs fix the ``meaning'' of
objects independently of the application.
The integration of various software packages is achieved by means of
OpenMath Phrasebooks; they convert OpenMath objects to and from the
software package's internal representation and determine the package's
actions. The translation is governed by the CDs and the specifics of
the software packages.
OpenMath Objects
We now focus on the abstract layer, where mathematical objects are
represented by labelled trees, called OpenMath objects or OpenMath
expressions. The formal definition of an abstract OpenMath object is
given below.
Definition 4.2.1
OpenMath objects are built recursively as follows.
- (i)
- Basic OpenMath objects, e.g., integers, IEEE floating point
numbers, Unicode character strings, byte-arrays, symbols (defined in
CDs) and variables, are OpenMath objects.
- (ii)
- If A1, ..., An (n > 0) are OpenMath objects, then
application
(A1,..., An)
is an OpenMath application object.
- (iii)
- If
S1,..., Sn are OpenMath symbols, and A, A1,
..., An, (n > 0) are OpenMath objects, then
attribution
(A, S1 A1, ... , Sn An)
is an OpenMath attribution object and A is the object
stripped of attributions. The operation of recursively
applying stripping to the stripped object is called flattening
of the attribution. When the stripped object after flattening
is a variable, the attributed object is called attributed
variable.
- (iv)
- If B and C are OpenMath objects, and v1, ...,
vn
(n
 0) are OpenMath variables or attributed variables,
then
0) are OpenMath variables or attributed variables,
then
binding
(B, v1,..., vn, C)
is an OpenMath binding object.
- (v)
- If S is an OpenMath symbol and A1, ..., An
(n
 0) are OpenMath objects, then
0) are OpenMath objects, then
error
(S, A1,..., An)
is an OpenMath error
object.
As mentioned earlier, OpenMath Content Dictionaries (CD) collect
and provide definitions of mathematical notions for usage within OpenMath
objects as described in Section 4.4. The official repository
for CDs is [33]. In this document we denote by
foo:bar the symbol with name bar defined in the CD
foo.
OpenMath abstract objects representing mathematical concepts are obtained
for instance by using the application constructor as in the
following examples.
Example 4.2.1
As a first example, consider the OpenMath object
A corresponding to
1 + 2,
application(arith1:plus, 1, 2)
where
arith1:plus is the symbol plus defined in the CD
arith1 and
1 and
2 represent basic objects (arbitrary length
integers).
Example 4.2.2
Applications can also be useful for representing algebraic structures.
Consider the polynomial ring
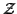 p[X]
p[X]. It is representable as
OpenMath abstract object like:
| application(polyr : PolynomialRingR,application(setname2 : Zm, p), x) |
|
|
(4.1) |
In this object, the OpenMath symbols
polyr:PolynomialRingR and
setname2:Zm identify the polynomial ring structure obtained
from the integers modulo
p. More precisely, they are the symbols
called
PolynomialRingR and
Zm defined in the CDs
polyr and
setname2, respectively.
Example 4.2.3
Now a slightly more complicated OpenMath object is given in
Figure
4.1, namely the one for
It involves,
amongst others, the CDs
arith1 for the symbols
e,
+,
-,
*,
/,
^ and
nums1 for
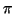
and imaginary
i.
Figure 4.1:
An OpenMath object built by binding and application.
|
|
OpenMath Encodings
OpenMath encodings map OpenMath objects to byte streams that can easily be
exchanged between processes or stored and retrieved from files.
Two major encodings supported and described by
the OpenMath Standard are
XML and binary. The first encoding uses only ISO 646:1983
characters [29] (ASCII characters) and is suitable
for sending OpenMath objects via e-mail, news, cut-and-paste, etc. and for
further processing by a variety of XML tools.
The second encoding is a custom-built binary encoding meant to be used when
compactness is crucial, for instance in interprocess communications
of very large objects over a network.
Example 4.3.1
For example, consider a polynomial with coefficients in the ring of
integers modulo some prime
p,
f = X3 - X + 1. It
can be represented in several ways as an abstract OpenMath object, either
as univariate or (degenerate) multivariate, as a sum of terms or vector
of coefficients etc. Supposing that we wish to represent
f recursively,
i.e. as a univariate polynomial whose coefficients are themselves
univariate polynomials and so on, by using the symbol
polyr:PolynomialR, It can be encoded in a human-readable
format using XML and stored as:
<OMOBJ><OMA><OMS cd="polyr" name="PolynomialR"/>
|
<OMA><OMS cd="polyr" name="PolynomialRingR"/>
<OMA><OMS cd="setname2" name="Zm"/>
<OMV name="p">
</OMA>
<OMV name="X"/>
</OMA>
|
<OMA><OMS cd="polyr" name="PolyRrep"/>
<OMV name="X"/>
<OMA><OMS cd="polyr" name="monomial"/>
<OMI> 3 </OMI><OMI> 1 </OMI>
</OMA>
<OMA><OMS cd="polyr" name="monomial"/>
<OMI> 1 </OMI><OMI> -1 </OMI>
</OMA>
<OMA><OMS cd="polyr" name="monomial"/>
<OMI> 0 </OMI><OMI> 1 </OMI>
</OMA>
</OMA>
</OMA>
</OMOBJ>
Reading from the encoding of the example, the outermost XML
element <OMOBJ> encloses nested OpenMath application objects,
appearing within the element <OMA>, which are built using
OpenMath symbols (<OMS>), OpenMath variables (<OMV>), and
integers (<OMI>). Notice that the application object
highligted in bold above
is essentially the XML encoding of the
polynomial ring expressed abstractly in equation (4.1).
When embedding XML encoded OpenMath objects into a larger XML
document one may wish, or need, to use additional features. For
example use of extra XML attributes to specify
XML Namespaces [32] or xml:lang attributes to specify the
language used in strings [24]. Also, the encoding used in the
larger document may not be UTF-8. In particular, if OpenMath is
used with applications that use the
>XML Namespace Recommendation
[32] then they should ensure that OpenMath elements
are in the namespace http://www.openmath.org/OpenMath. This is
most conveniently achieved by adding the namespace declaration
xmlns="http://www.openmath.org/OpenMath" as an attribute to each
OMOBJ element in the document.
OpenMath Content Dictionaries
A Content Dictionary holds the meanings of (various)
mathematical `words' referred to as symbols. A set of official
CDs, each covering a specific area has been produced and is available
from the CD repository of the OpenMath society. Content Dictionaries may
be grouped into CD groups, so that applications can easily
refer to collections of Content Dictionaries. For instance, the
MathML CD group covers essentially the same areas of
mathematics as the content elements of the MathML
recommendation [12].
While OpenMath objects are built using symbols defined in some Content
Dictionary that is part of an ever growing collection of Content
Dictionaries, MathML makes explicit a relatively small number of
commonplace mathematical constructs chosen within the K-12 realm of
applications and, in addition, it provides the content symbol
(csymbol) to introduce a new symbol whose semantics is not
part of the core content elements of MathML. In particular, such an
external definition may reside in an OpenMath Content Dictionary as in
the following example.
Example 4.4.1
Consider the OpenMath abstract object of Example
4.2.2. It
can be expressed in MathML by introducing
csymbol where an
OpenMath symbol is needed in the encoding and is not supplied by the
core MathML elements.
MathML supports an extensive library of presentation symbols to
accomodate even the fanciest notation used by mathematicians. In this
respect, MathML (presentation) is the preferred choice for rendering
mathematical content and as such it is to be hoped that it will be
soon be supported by tools such as browsers and editors.
Users may submit their private CDs for public use. Before they can be
adopted as official OpenMath CD they undergo a refereeing process by
appointed members of the OpenMath Society. Details of this process
along with advice and tips for CD authors are contained in the document
On Writing Content Dictionaries.
CDs hold two types of information: that which applies to the
whole CD (appears in the header of the CD), and that which is
only relevant to a particular symbol definition (appears in a CD
Definition). Information pertinent to the whole CD includes the name,
a description, an expiration date, the status of the CD (official,
experimental, private, obsolete), and an optional list of CDs on which it
depends. Information restricted to a particular symbol includes a
name and a description in natural language. Optional information includes
examples of the use of this symbol, and formal properties satisfied by
this symbol which can be expressed as OpenMath objects or as plain text.
A browsable version of the set of content dictionaries produced in the
project can be found
here, while the latest official
CDs can be found on the
OpenMath Society website.
Although OpenMath does not enforce formal specification of symbols by
using signatures and axiomatic definitions, it recognizes their
advantages and leaves room to adopt them if required. In particular,
formal signatures in a specific type system can be used to assign
mathematical meaning to OpenMath objects in such a way that validation of
objects depends exclusively on the context determined by the CDs and
on some type information carried by the objects themselves. Formal
signatures and definitions are collected in additional files that can
be associated to a Content Dictionary. Signatures of symbols are
expressed in Signature files by OpenMath objects representing
types in a certain type system.
Light-weight Simple Type System
The Small Type System for OpenMath signatures has been designed according
to two requirements.
- Tools which read ``new'' CDs automatically, e.g. a search engine
which suddenly encountered as a symbol from a CD that it did not
recognise. In the context of a ``Small'' type system, there is
little more that can be offered to such systems than arity checking.
- Human beings reading the whole of a CD's fields, to determine
how they ought to implement the CD, either as OpenMath-reading software,
or, more interestingly, as OpenMath-writing software. These humans need
to interpret the symbols in a way that cannot be totally formalised.
However they ``ought to be'' imbued with that nebulous quality of
``common sense''.
To meet these goals, a system that encodes arity (and a little more)
in a totally formal way, but leaves clues in names etc. that should
help the human reader has been used, see
A Small OpenMath Type System
[27] for details.
Calculus of Constructions
More formal signatures can also be associated to OpenMath symbols with
the goal in mind of certifying the meaningfullness of OpenMath objects.
For instance in [18], extensions of the
Calculus of Constructions (CC) have been chosen as a starting point
for assigning signatures to OpenMath symbols because they are expressive,
well suited to modeling
algebra [13,9,31], and have decidable
type inference. Freely available software packages like Lego or
COQ [30,25] have implemented the necessary
functionality for performing type checks on OpenMath objects.
For more details see
A Type System For OpenMath.
Axiomatic definitions in a specific formal system are expressed as
OpenMath objects in DefMP (defining mathematical property) files.
More details are to be found in [19].
Example 4.4.2
Consider a private CD,
pock defining symbols needed in
an application dealing with primality testing. Beside giving a
natural language description, the author may introduce a new
symbol
pock:divides by a formal definition in terms of
the
DefMP representing the expression
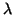 n :
n :  .
.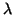 m :
m :  .(
.( q :
q :  ) n = qm
) n = qm:
binding(lc:Lambda,
attribution(n, icc:type, setname:N),
attribution(m, icc:type, setname:N),
binding(quant1:exists,
attribution(q, icc:type, setname:N),
application(relation1:eq,
n,
application(arith1:times, m, q))))
OpenMath Phrasebooks
The programs that act as an interface between a software system and
OpenMath are called phrasebooks. Their task is to translate the
OpenMath object, as understood by means of Content Dictionaries, to the
corresponding internal representation used by the specific software
package.
Figure 4.2:
General structure of an OpenMath phrasebook
|
|
Phrasebooks providing an interface to and from OpenMath have been built into
experimental versions of both AXIOM and GAP, cf.
[21,22]. These are examples in which the software
package itself provides the interface to and from OpenMath internally.
A Mathematica phrasebook based on the OpenMath C library
is available at INRIA.
Notice that the OpenMath phrasebooks are mainly concerned with the
translation between OpenMath objects and internal system-specific
representation. The interpreted behavior for most computer algebra
packages receiving an OpenMath object is an evaluation. For instance,
upon input of the object application(integer:rem,
application(integer:gcd, 12, 3), 2) Mathematica
would output 1.
In general, control of the interaction with a software package is not
ruled by the existing OpenMath libraries. For this task, OpenMath allows
freedom of choice between several
paradigms [14,28].
Translation tools [15] have been produced which map between
the common
subset of mathematics covered by MathML-Content and the OpenMath CD
group MathML. For displaying OpenMath objects with
Presentation MathML, one may use xsl stylesheets driven by OpenMath
CDs. Sample stylesheets are available from the OpenMath Society web
pages.
OpenMath compliancy is desirable as a means to maximize the potential for
interoperability amongst OpenMath applications. To be OpenMath
compliant an application has to fullfill requirements dealing with
the encoding it can accept or generate, with the declaration and
handling of CDs it understands and with the error behaviour. The
detailed description of compliancy is part of the
standard
[23].



Next: OpenMath and MathML
Up: The OpenMath Project Final
Previous: Technical Summary
Contents
The OpenMath Consortium

 0) are OpenMath variables or attributed variables,
then
binding (B, v1,..., vn, C)is an OpenMath binding object.
0) are OpenMath variables or attributed variables,
then
binding (B, v1,..., vn, C)is an OpenMath binding object. 0) are OpenMath objects, then
error (S, A1,..., An)
0) are OpenMath objects, then
error (S, A1,..., An)
![\includegraphics [scale=0.75]{phrasebook}](img12.gif)
