Chapter 1
Introduction to OpenMath

1.1 OpenMath Architecture

Figure 1.1 The OpenMath Architecture

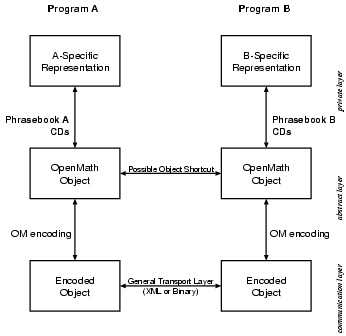
The architecture of OpenMath is described in Figure 1.1 and summarizes the interactions among the different OpenMath components. There are three layers of representation of a mathematical object . The first is a private layer that is the internal representation used by an application. The second is an abstract layer that is the representation as an OpenMath object. Note that these two layers may, in some cases, be the same. The third is a communication layer that translates the OpenMath object representation into a stream of bytes. An application dependent program manipulates the mathematical objects using its internal representation, it can convert them to OpenMath objects and communicate them by using the byte stream representation of OpenMath objects.

1.2 OpenMath Objects and Encodings

OpenMath objects are representations of mathematical entities that can be communicated among various software applications in a meaningful way, that is, preserving their "semantics".

OpenMath objects and encodings are described in detail in Chapter 2 and Chapter 3.

The standard endorses two encodings in XML and binary formats. At the time of writing, these are the encodings supported by most existing OpenMath tools and applications, however they are not the only possible encodings of OpenMath objects. Users who wish to define their own encoding , are free to do so provided that there is a well-defined correspondence between the new encoding and the abstract model defined in Chapter 2.

1.3 Content Dictionaries

Content Dictionaries (CDs) are used to assign informal and formal semantics to all symbols used in the OpenMath objects. They define the symbols used to represent concepts arising in a particular area of mathematics.

The Content Dictionaries are public, they represent the actual common knowledge among OpenMath applications. Content Dictionaries fix the "meaning" of objects independently of the application. The application receiving the object may then recognize whether or not, according to the semantics of the symbols defined in the Content Dictionaries, the object can be transformed to the corresponding internal representation used by the application.

1.4 Additional Files

Several additional files are related to Content Dictionaries. Signature Dictionaries contain the signatures of symbols defined in some OpenMath Content Dictionary and their format is endorsed by this standard.

Furthermore, the standard fixes how to define a specific set of Content Dictionaries as a CDGroup.

Auxiliary files that define presentation and rendering or that are used for manipulating and processing Content Dictionaries are not discussed by the standard.

1.5 Phrasebooks

The conversion of an OpenMath object to/from the internal representation in a software application is performed by an interface program called a Phrasebook. The translation is governed by the Content Dictionaries and the specifics of the application. It is envisioned that a software application dealing with a specific area of mathematics declares which Content Dictionaries it understands. As a consequence, it is expected that the Phrasebook of the application is able to translate OpenMath objects built using symbols from these Content Dictionaries to/from the internal mathematical objects of the application.

OpenMath objects do not specify any computational behaviour, they merely represent mathematical expressions. Part of the OpenMath philosophy is to leave it to the application to decide what it does with an object once it has received it. OpenMath is not a query or programming language. Because of this, OpenMath does not prescribe a way of forcing "evaluation" or "simplification" of objects like 2+3 or sin(π). Thus, the same object 2+3 could be transformed to 5 by a computer algebra system, or displayed as 2+3 by a typesetting tool.